مساحة المعين
محتويات المقال
محتويات
- ١ تعريف المعين
- ٢ المعين و المربع
- ٣ المعين و متوازي الأضلاع
- ٤ قانون حساب مساحة المعين
تعريف المعين
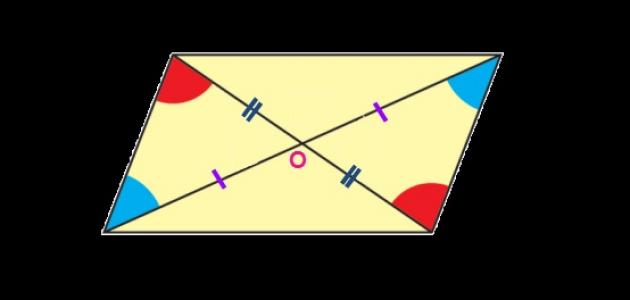
المعين هو شكل من الأكال الهندسية و هو من الأشكال الرباعية أي المعين هو شكل رباعيو عدد أضلاعه أربعة ، تتميز جميع أضلاعه متساوية ، و فيه كل زاويتين متقابلتين متساويتين ، و كل ضلعين متقابلين متوازين ، و عدد أقطارين إثنين و هو ما يميزه بإنه متعامدين .
المعين و المربع
يختلف المربع عن المعين بأن عدد أضلاع أربعة متساوية في الطول كما هي في المعين لكن المعين كل ضلعين متوازيين متساووين في الطول بينما المربع أضلاعه قائمة و يصنع زوايا قائمة أي كل زاوية قياسها في المربع تسعون درجة بينما بالمعين لا تشكل زواياه من زوايا القائمة .
المعين و متوازي الأضلاع
المعين هو شكل يشبه متوازي الأضلاع و لكن المعين كل أضلاعه متساوية في الطول و لكن متوازي الأضلاع أضلاعه الأربعة غير متساوية في الطول ، بينما المعين كل ضلعين متوازيين متساووين في الطول و متوازي الأضلاع كل ضلعين متقابلين متساووين في الطول ، أما من ناحية الزوايا في متوازي الأضلاع كل زاويتين متجاورتين متساويتين في القياس و المعين كل زوايتين متقابلتين متساويتين في القياس بينما الزاويا المتجاورة غير متساوية في القياس .
قانون حساب مساحة المعين
هناك قانون لا نتجاهله في قياس و حساب مساحة المعين و هو حاصل ضرب القطر الأول في القطر الثاني تقسيم العدد 2.( طول القطر الأول × طول القطر الثاني ÷2 ) مثال، معين طول قطره الأول 7سم و طول قطره الثاني 8 سم أوجد مساحة المعين . نجد مساحة المعين كما يلي نجد حاصل ضرب القطر الأول في القطر الثاني أي نتبع في الحساب باستخدام قاعدة و قانون حساب مساحة المعين و يكون العدد 7 × 8 يساوي 56 و هذا الناتج يقسم على العدد 2 و تكون مساحة المعين 56 ÷ 2 يساوي 28 سم2 .
يعتبر المعين هو عبارة عن مثلثين متساويين في الأضلاع أي مثلث متساوي الساقين عدد 2 مطبوقين على بعض مشتركين في نفس طول القاعدة لكن عند الرسم نخفي هذه القاعدة و لكن عند الحساب نظهر هذه القاعدة و نعتمد عليها القياس ، و لذلك نعتمد على مساحد أحد المثلثين في حساب مساحة المعين و لحساب مساحة مثلث متساوي الساقين يجب أن يكون متوفر في القياس طول القاعدة و طول الإرتفاع المتعامد على هذه القاعدة ، مثال: احسب مساحة معين إذا علمت إنه يحتوي على مثلث متساوي الساقين طول القاعدة فيه تساوي 7 سم و طول إرتفاع المثلث 4 سم ؟ نتبع قاعدة حساب مساحة مثلث متساوي الساقين ( طول القاعدة × طول الإرتفاع المتعامد على المعين ) نطبق على القانون ( 7 ×4 ) يساوي 28 سم 2 أي مساحة المعين تساوية 28 سم2 و هو نفس نتيجة المثال الأول أعلاه .